Antwort Co platí pro Rovnoramenny Trojuhelnik? Weitere Antworten – Co platí pro rovnoramenný trojúhelník
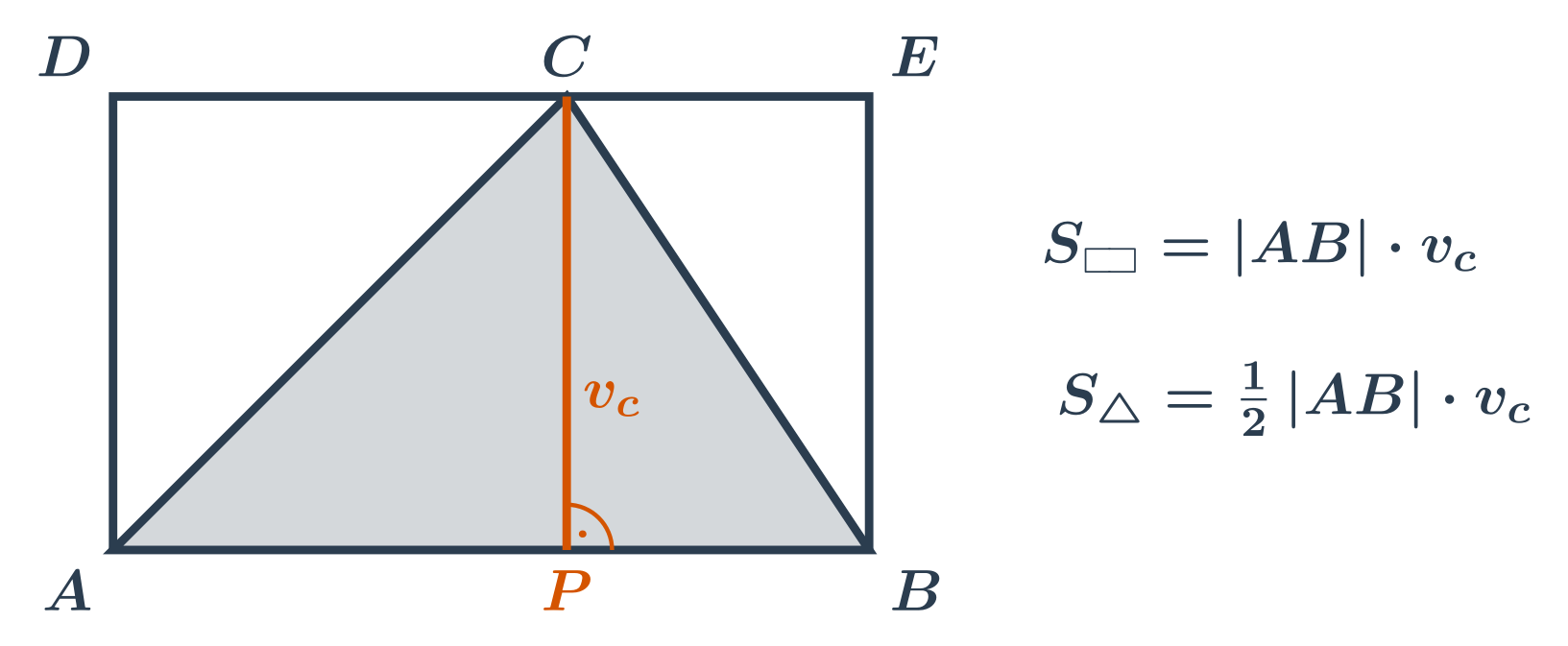
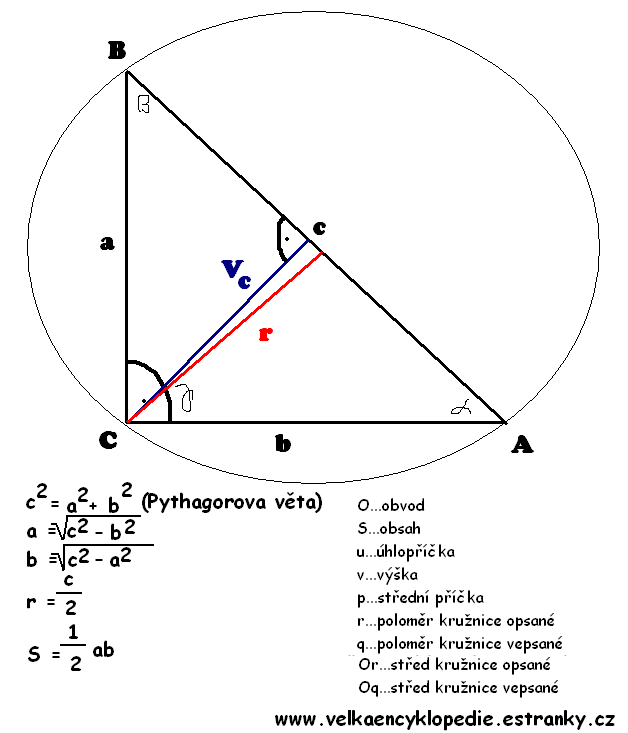
Kromě vlastností společných pro každý trojúhelník má rovnoramenný trojúhelník navíc tyto vlastnosti: Je osově souměrný podle osy procházející hlavním vrcholem a středem základny. Úhly při základně jsou shodné. Výšky příslušné ramenům jsou shodné.To je pythagorova věta – c^2=a^2+b^2, kde c je rameno, a je výška a b polovina základny (výška v rovnoramenném trojúhelníku půlí základnu).Výpočet obsahu libovolného trojúhelníku je polovina součinu stran a výšky na tu stranu.
Co je rovnostranný Trojuhelnik : Rovnostranný trojúhelník je trojúhelník, který má všechny tři strany shodné.
Co platí pro rovnostranný trojúhelník
Rovnostranný trojúhelník můžeme otočit o 120° a úhly přesune jeden na druhý ⇒ všechny vnitřní úhly jsou shodné. Všechny strany rovnostranného trojúhelníku jsou rovnocenné ⇒ všechny úhly rovnostranného trojúhelníku musí být také rovnocenné.
Co to je rovnoramenný trojúhelník : Rovnostranný trojúhelník – všechny strany a vnitřní úhly jsou shodné. Rovnoramenný trojúhelník – má shodná ramena a úhly při základně. sss – dva trojúhelníky jsou shodné, shodují-li se ve všech třech stranách. sus – dva trojúhelníky jsou shodné, shodují-li se ve dvou stranách a úhlu jimi sevřeném.
Úsečka je osově souměrná a má v rovině jedinou osu souměrnosti (kolmici v jejím středu). Rovnoramenný trojúhelník je osově souměrný. Trojúhelník, který není rovnoramenný, není osově souměrný. Všechny pravidelné mnohoúhelníky jsou osově souměrné.
V pravoúhlém trojúhelníku platí, že velikost plochy čtverce nad odvěsnou je stejná jako plocha obdélníku (vztyčeného výškou) ve čtverci nad odvěsnou. Pythagorova věta: V každém pravoúhlém trojúhelníku je součet obsahů čtverců nad odvěsnami stejný jako obsah čtverce nad přeponou.
Kolik má Rovnostranný trojúhelník os souměrnosti
Osově souměrné útvary
Rovnostranný trojúhelník je osově souměrný podle tří os určených výškami/těžnicemi trojúhelníka (u rovnostranného trojúhelníka tyto úsečky splývají), čtverec podle čtyř os (obr. 3.2.1), kosočtverec podle dvou os určených úhlopříčkami, obdélník podle dvou os.Rovnostranný trojúhelník má všechny strany stejně dlouhé. Zároveň platí, že všechny vnitřní úhly mají velikost 60 stupňů. Rovnoramenný trojúhelník má dvě strany stejně dlouhé a třetí strana má délku jinou.Obdélník je v obecném případě osově souměrný podle dvou os. Osami souměrnosti jsou rovnoběžky se stranami procházející průsečíkem úhlopříček. Speciální případ obdélníku – čtverec – je osově souměrný podle čtyř os, dalšími dvěma osami jsou jeho úhlopříčky.
Každý trojúhelník má tři výšky. Menší straně odpovídá větší výška. Přímky, na nichž leží výšky, se protínají v jednom bodě, který se nazývá ortocentrum nebo také výšiště. Ortocentrum leží uvnitř trojúhelníku, pokud je ostroúhlý.
Co plati pro úhlopříčky v obdélníku : Úhlopříčky obdélníku se půlí a jsou stejně dlouhé. Obdélníku lze opsat kružnici se středem v průsečíku úhlopříček a poloměrem rovným polovině délky úhlopříčky. Obdélníku nelze vepsat kružnici – výjimkou je pouze speciální případ obdélníku – čtverec. Obdélník je středově souměrný podle průsečíku úhlopříček.
Co znamená osově souměrné : Osově souměrný útvar je takový útvar, který se podle nějaké své osy zobrazí sám na sebe. Mezi osově souměrné útvary patří například rovnostranný trojúhelník, čtverec, kosočtverec, obdélník, kružnice.
Jak se hleda těžiště trojúhelníku
Těžiště se vždy nachází uvnitř trojúhelníku.
To znamená, že dvě třetiny délky těžnice jsou na jedné straně od těžiště a zbývající jedna třetina na další straně. Delší část těžnice je vždy směrem „k vrcholu“ trojúhelníku. „U strany“ je naopak kratší část.
Pokud má čtyřúhelník dvě dvojice protějších stran rovnoběžných, nazývá se rovnoběžník. Každé dva jeho sousední úhly dávají součtem úhel přímý, protilehlé úhly jsou shodné, stejně jako délky protilehlých stran. Úhlopříčky se v rovnoběžníku navzájem půlí.VLASTNOSTI LICHOBĚŽNÍKŮ
1) Délka střední příčky se rovná polovině součtu délek obou základen. 2) Součet velikostí vnitřních úhlů přilehlých k ramenu lichoběžníku je 180°. 3) Vzdálenost přímek, na kterých leží základny, je výška lichoběžníku. 4) Součet vnitřních úhlů je 360°.
Jak poznat osovou souměrnost : Osově souměrný útvar je takový útvar, který se podle nějaké své osy zobrazí sám na sebe. Mezi osově souměrné útvary patří například rovnostranný trojúhelník, čtverec, kosočtverec, obdélník, kružnice.